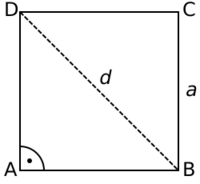
Сторона квадрата равна а найдите отношение

Окружности в квадрате и квадраты в окружности
Английский язык Математика. Русский язык Английский язык Математика. Русский язык Английский язык Математика Биология. Английский язык Биология Физика Химия. Английский язык Биология Химия. Главная Математика 6 класс Математика, 6 класс, Дорофеев Г.
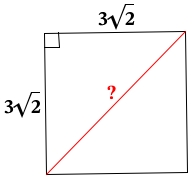



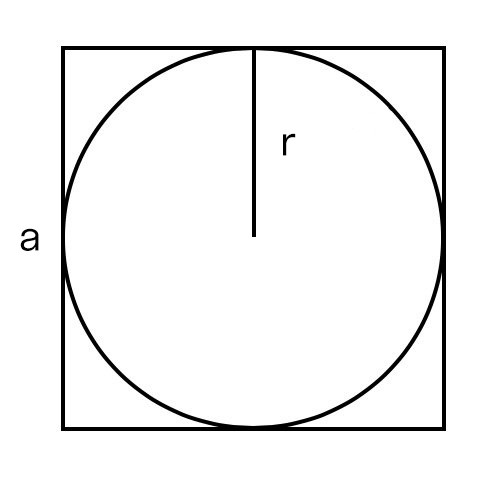
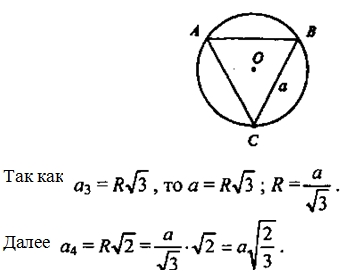

Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины. Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры.
- Квадрат часто называют правильным четырехугольником, потому что его углы и стороны равны. Давайте разберемся, какие формулы помогут найти его площадь, чтобы решать задачи быстро и легко.
- В вашем браузере отключен JavaScript. Из-за этого многие элементы сайта не будут работать.
- Содержание переместить в боковую панель скрыть.
- Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
- В статье, которую можно прочитать по ссылке, приведены решения пяти задач. К двум окружностям радиусов R и r , касающихся друг друга внешним образом, проведена общая внешняя касательная.
- Подобрать занятия.
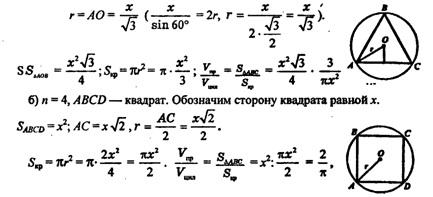



Поэтому Таким же образом. Значит, четырехугольник LMNK есть квадрат. Стороны квадрата разделены в отношении m к n , причем к каждой вершине прилежит один большой и один малый отрезок. Последовательные точки деления соединены прямыми. Найти площадь полученного четырехугольника, если сторона данного квадрата равна а. Другое решение.