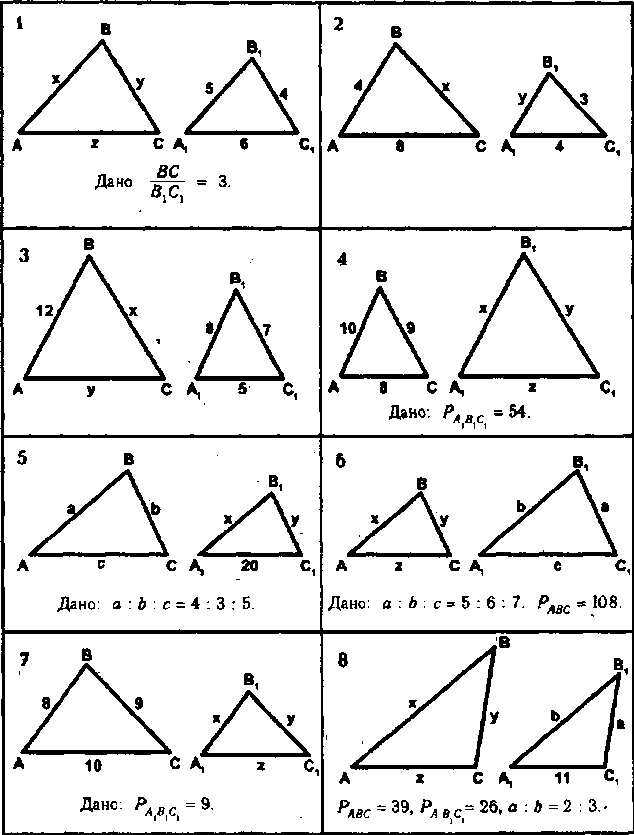
Найти на рисунке подобные треугольники

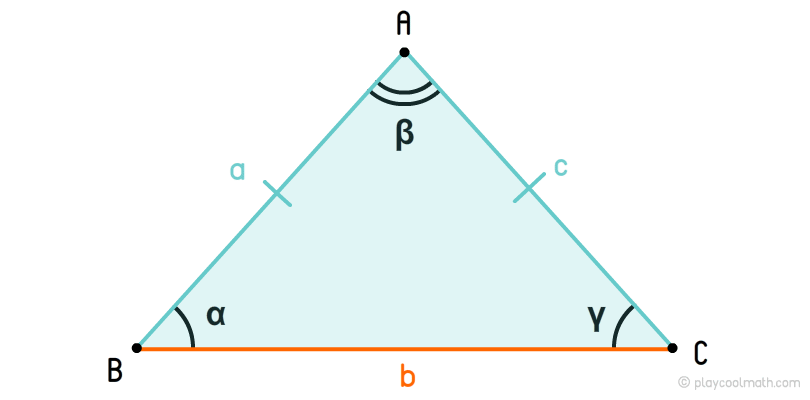
Подобные треугольники
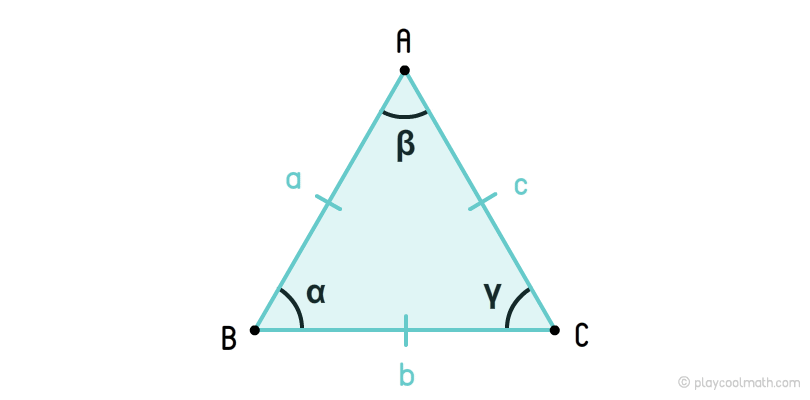
Две фигуры и называются подобными, если они переводятся друг в друга преобразованием подобия, то есть таким преобразованием, при котором расстояния между точками изменяются увеличиваются или уменьшаются в одно и то же число раз. Если фигуры и подобны, то пишется. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны и соответствующие отрезки пропорциональны.




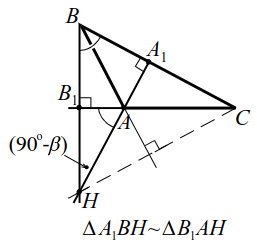




Признаки подобия треугольников Пропорциональные отрезки в прямоугольных треугольниках Соотношение между сторонами и углами прямоугольного треугольника Окружность. Касательная к окружности Центральные и вписанные углы Четыре замечательные точки треугольника Вписанная и описанная окружности. Вы повторите тему "Признаки подобия треугольников"; Познакомитесь с понятием "среднее пропорциональное"; Научитесь находить элементы прямоугольного треугольника и решать соответствующие задачи. Перед началом обучения обязательно распечатайте материал для работы нажмите на изображение ниже :.
.png)

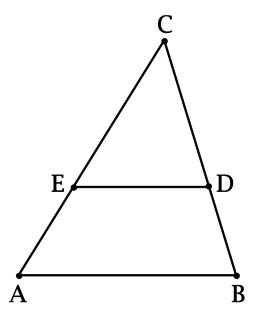

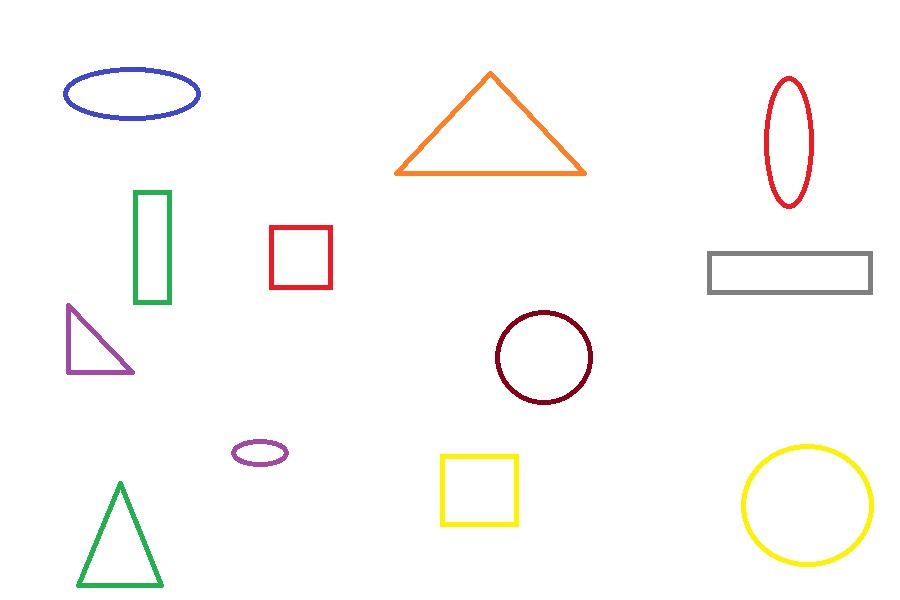
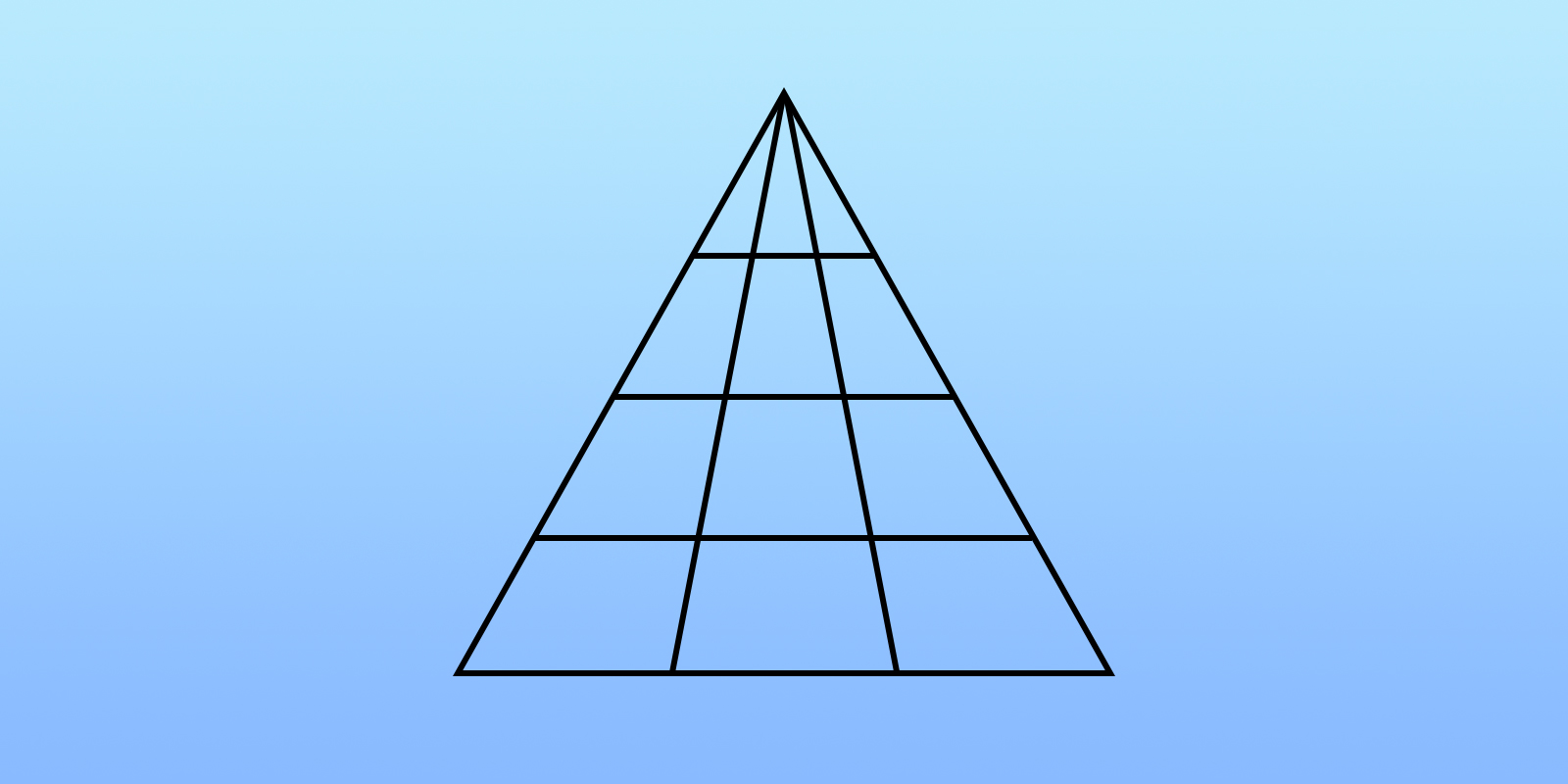


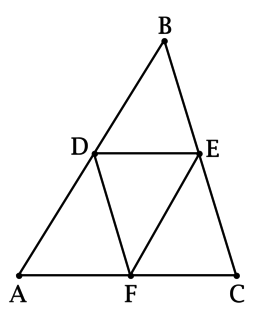


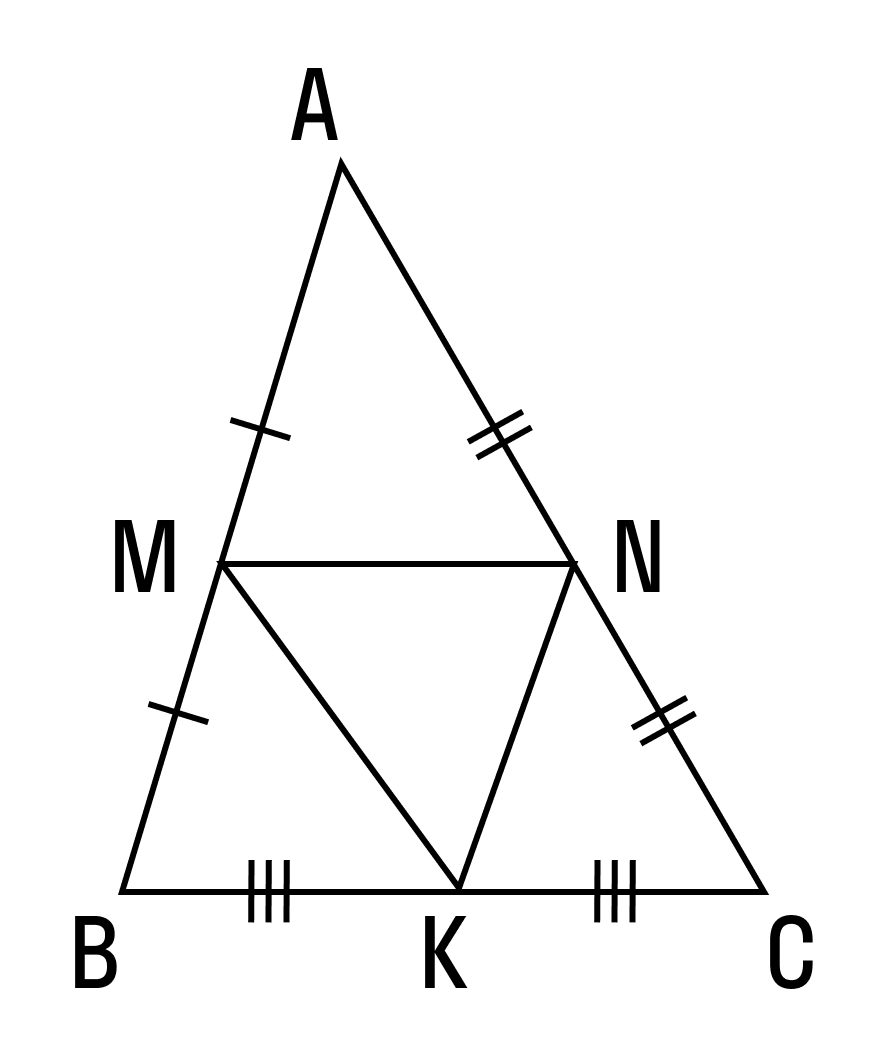
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно. Если две стороны треугольника пересекает прямая, параллельная третьей стороне рис. По первому признаку эти треугольники подобны. И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции. Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон.