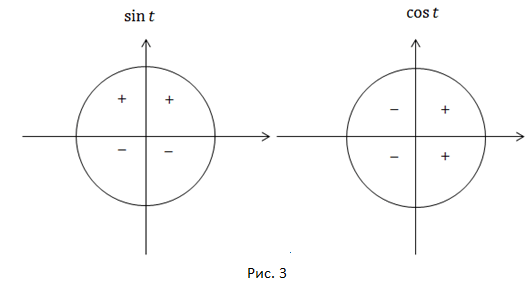
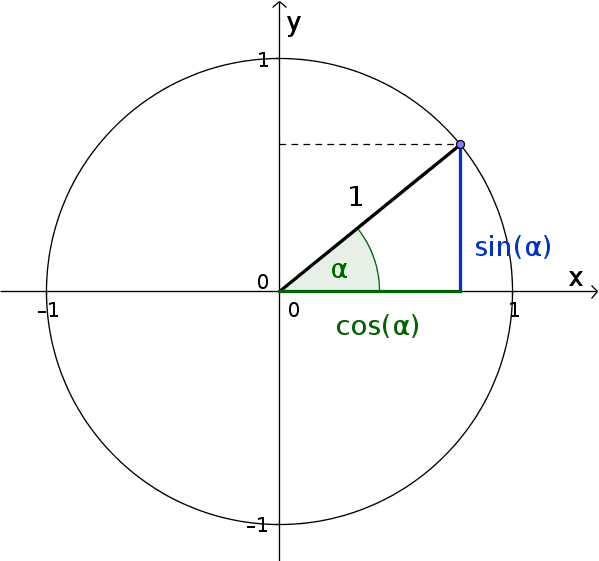
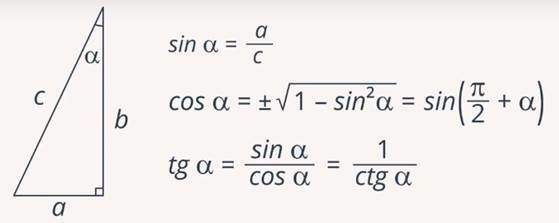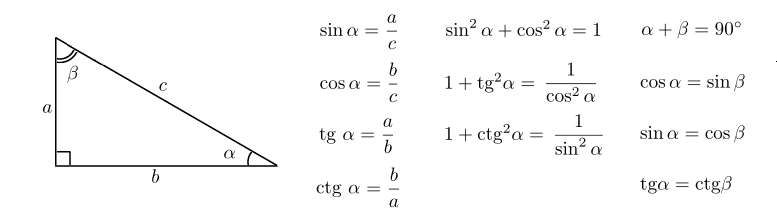Как называется отношения синуса и косинуса
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
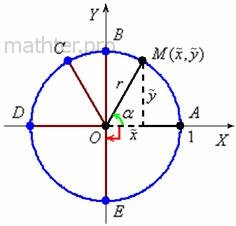
Данный термин впервые появился в г. Тригонометрические вычисления применяются практически во всех областях геометрии , физики и инженерного дела. Например, большое значение имеет техника триангуляции , позволяющая измерять расстояния до недалёких звёзд в астрономии , между ориентирами в географии , контролировать системы навигации спутников. Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду.




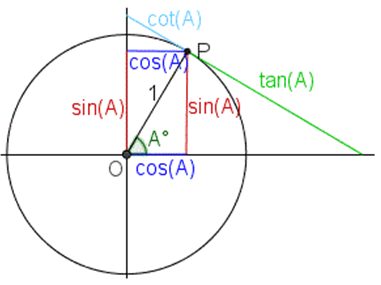
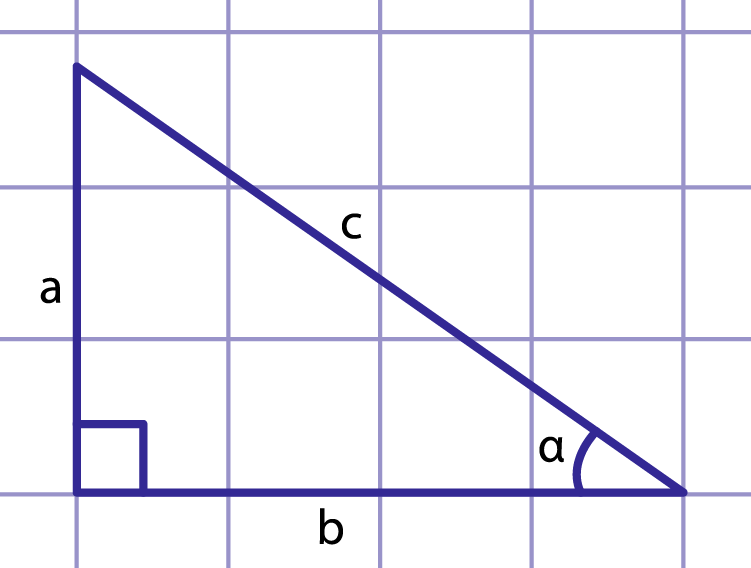
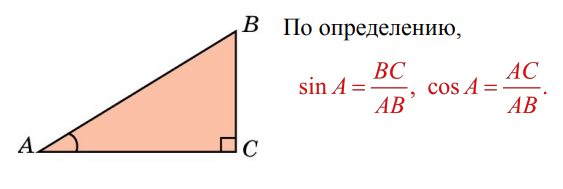
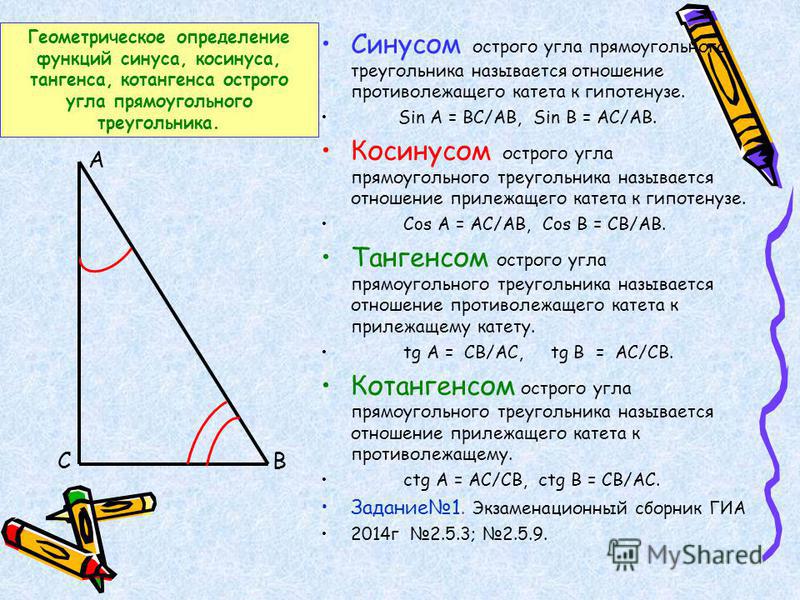
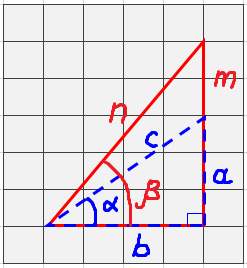
Прямоугольным треугольником , называется треугольник у которого один из углов прямой составляет 90 градусов. Две стороны которые прилежат к прямому углу, называются катетами , а сторона лежащая напротив прямого угла, называется гипотенузой. Тангенс tg a — это отношение противолежащего катета к прилежащему катету; Другое равносильное определение: тангенсом острого угла называется отношение синуса угла к его косинусу;. Котангенс ctg a — это отношение прилежащего катета к противолежащему.
- Нахождение обратных тригонометрических соотношений
- Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
- В данном материале, мы изучим основное определение тригонометрии , какие свойства ей характерны, применение в математике, приведем примеры решения уравнений.
- Чтобы хорошо разобраться в этих понятиях нет, не в чёрте!
- Как это всё запомнить?
- Кирилл Хисматов. Суть всех 12 тригонометрических функций.
- Содержание переместить в боковую панель скрыть. Первый раз термин появился в году в виде названия книги немецкого математика Бартоломеуса Питискуса — [2].
- Удобная навигация, видео-разборы тем, задачи для самопроверки — всё это в вашем кармане. А ещё раздел с полезными материалами, календарь занятий и уведомления о предстоящих уроках.





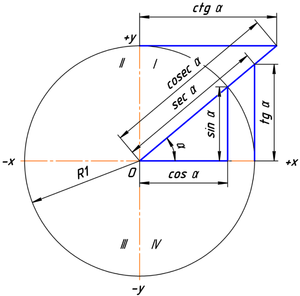
Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число. Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией. До Второй мировой войны в Германии и во Франции эти функции обозначались так же, как принято в русскоязычных текстах [2] , но потом в литературе на языках этих стран был принят англоязычный вариант записи тригонометрических функций. Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции версинус и т.